SQL puzzle II.

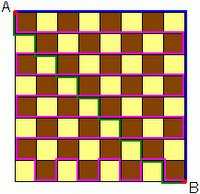
The second one. I'd call it "Google's puzzle" -- a friend of a colleague of mine defined it like this: suppose we have a chessboard and two points "A" and "B" defined. The goal is two find all possible routes from left-upper corner, point "A" to the right-bottom one, point "B". Cell's edges are the only way to move from point "A" to "B". Definitely there would be optimal routes and non-optimal ones. The picture shows two optimal routes (blue and green) and one non-optimal (pink). One can solve this task using any programming language, but I decided to solve it using SQL! Below you can find a solution for the 2x2 chessboard. I won't suggest to execute this query to calculate all routes for 8x8 -- it would be very expensive. However it's ok to calculate the number of optimal routes only, you would have to modify the query though :-)

SQL> CREATE TABLE chessboard (y INTEGER, x INTEGER);

Table created.

SQL> VARIABLE s NUMBER;
SQL> EXEC :s := 2;

PL/SQL procedure successfully completed.

SQL> DECLARE
2    chessboard_size                  NUMBER := :s;
3  BEGIN
4    DELETE chessboard;
5    FOR y IN 0..chessboard_size
6    LOOP
7      FOR x IN 0..chessboard_size
8      LOOP
9        INSERT INTO chessboard(y, x) VALUES(y, x);
10      END LOOP;
11    END LOOP;
12    COMMIT;
13  END;
14  /

PL/SQL procedure successfully completed.

SQL> COLUMN chessboard FORMAT A30
SQL> COLUMN optimal FORMAT 9999
SQL> COLUMN path FORMAT A50
SQL> SELECT LTRIM(SYS_CONNECT_BY_PATH(y || ':' || x, ' ')) chessboard
2    FROM chessboard
3   WHERE LEVEL = (SELECT MAX(x) + 1 FROM chessboard)
4   START WITH x = 0
5  CONNECT BY x > PRIOR x AND y = PRIOR y
6  /

CHESSBOARD
------------------------------
0:0 0:1 0:2
1:0 1:1 1:2
2:0 2:1 2:2

SQL> SELECT optimal
2       , path
3    FROM (
4         SELECT LEVEL optimal
5              , SYS_CONNECT_BY_PATH(y || ':' || x, ' ') path
6           FROM chessboard
7          START WITH y = 0 AND x = 0
8        CONNECT BY NOCYCLE
9                1 = CASE
10                      WHEN PRIOR x = :s AND PRIOR y = :s
11                        THEN 0
12                        ELSE CASE
13                               WHEN (y - 1 = PRIOR y AND x = PRIOR x)
14                                 OR (y + 1 = PRIOR y AND x = PRIOR x)
15                                 OR (x - 1 = PRIOR x AND y = PRIOR y)
16                                 OR (x + 1 = PRIOR x AND y = PRIOR y)
17                               THEN 1
18                             END
19                    END
20         )
21   WHERE path LIKE '% ' || TO_CHAR(:s, 'FM99') || ':' || TO_CHAR(:s, 'FM99')
22   ORDER BY optimal
23  /

OPTIMAL PATH
------- --------------------------------------------------
5  0:0 0:1 0:2 1:2 2:2
5  0:0 0:1 1:1 1:2 2:2
5  0:0 1:0 1:1 1:2 2:2
5  0:0 1:0 2:0 2:1 2:2
5  0:0 1:0 1:1 2:1 2:2
5  0:0 0:1 1:1 2:1 2:2
7  0:0 0:1 0:2 1:2 1:1 2:1 2:2
7  0:0 1:0 2:0 2:1 1:1 1:2 2:2
7  0:0 1:0 1:1 0:1 0:2 1:2 2:2
7  0:0 0:1 1:1 1:0 2:0 2:1 2:2
9  0:0 0:1 0:2 1:2 1:1 1:0 2:0 2:1 2:2
9  0:0 1:0 2:0 2:1 1:1 0:1 0:2 1:2 2:2

12 rows selected.

[It's 12870 for 8x8 board (O=(n*2)!/(n!)^2)]